
Sentencian al expolítico Javier López a 60 años de prisión por el feminicidio de la activista Cecilia Monzón
El excandidato del PRI a gobernador de Puebla, Javier López Zavala, fue sentenciado a 60 años de prisión como autor intelectual del feminicidio de su expareja, la abogada Cecilia Monzón.
Además del expolítico, también fueron sentenciados a la misma condena Jair Mauricio Domínguez y Silvestre Vargas Ruiz, quienes dispararon contra la también activista en mayo de 2022.
En un comunicado, la Fiscalía de Puebla informó que “la resolución judicial es resultado de una investigación integral, exhaustiva y técnicamente sustentada, en la cual el Ministerio Público logró acreditar plenamente la responsabilidad penal de los sentenciados mediante la presentación de pruebas sólidas y suficientes, las cuales fueron valoradas por el Tribunal durante el desarrollo del juicio oral”.
Tras la Audiencia de Individualización de Sanciones y Reparación del Daño, el Tribunal emitió su determinación, imponiéndole 60 años de prisión a Javier N., como autor intelectual y 60 años de prisión contra Silvestre N. y Jair N., como autores materiales.
Además deberán pagar una multa de 1000 Umas, el pago de la reparación del daño moral por 3,000 Umas y 1,200 Umas de Indemnización.

El pasado 23 de diciembre, la familia Monzón detalló en un comunicado que el Tribunal de Enjuiciamiento con Perspectiva de Género de la ciudad de Puebla dictó sentencia condenatoria acreditando que López Zavala fue quien planificó el feminicidio de la abogada y proveyó los medios materiales para la ejecución del crimen.
Asimismo, indicó que se estableció la culpabilidad de Jair Mauricio Domínguez, sobrino de López Zavala, y Silvestre Vargas Ramírez como coautores materiales, responsables de disparar en hasta siete ocasiones contra Cecilia.
Puedes leer: Feminicidio de Cecilia Monzón cumple tres años; es un recordatorio de la violencia institucional, señalan activistas
Por lo que la familia y equipo legal buscaban la pena máxima de 60 años de prisión, la cual fue otorgada este miércoles.
La petición de las penas máximas surge tras un juicio extenuante que inició en abril de 2025 y abarcó más de ochenta audiencias.
A pesar de que la defensa de los imputados interpuso “múltiples recursos legales” con el objetivo de retrasar el procedimiento, el tribunal emitió una resolución detallada que individualiza la responsabilidad de cada implicado.

Feminicidio de Cecilia Monzón
Cecilia Monzón fue asesinada el 21 de mayo de 2022 en el municipio de San Pedro Cholula, Puebla, cuando viajaba en su vehículo y fue alcanzada por dos sujetos en motocicleta; uno de ellos le disparó en seis ocasiones.
La Fiscalía estatal identificó como presuntos responsables a Javier López Zavala, quien también fue candidato a la gubernatura del estado en 2010 por el PRI; y a dos personas más.
También lee: Cecilia Monzón recibe justicia por violencia familiar, pero su feminicidio sigue sin sentencia
A finales de mayo de 2025, Javier “N” fue declarado culpable del delito de violencia familiar en agravio de la abogada y activista, pero la sentencia por su presunta responsabilidad en el feminicidio continuaba pendiente.
En noviembre, un Tribunal de Puebla revocó el fallo por violencia familiar contra López Zavala, dejó sin efecto su sentencia y ordenó repetir la audiencia. En ese momento, la familia de Monzón manifestó que dicho tribunal es “arbitrario”, ya que su operación “es grave y roza con la ignorancia” en lo que respecta a conocimientos legales en el ámbito penal.
En diciembre de 2025 el juez determinó la responsabilidad del excandidato a gobernador de Puebla y dos personas más.
Relacionado

Envolver regalos de Navidad con formas irregulares siempre es un dolor de cabeza, pero aquí tienes la fórmula para un envoltorio perfecto.
Sin embargo, para la mayoría de quienes no somos expertos en envolver regalos, lo más probable es que el resultado final sea un envoltorio caótico, un revoltijo de papel y cinta adhesiva.
Probablemente por eso envolver regalos de Navidad no suele ser una tarea que muchos disfruten.
Pero este año quizás quieras añadir una regla y una calculadora a tus materiales para envolver regalos. Es hora de aplicar el poder de las matemáticas esta Navidad.
Pensar de forma innovadora
Quizás el artículo más fácil de envolver sean las cajas cúbicas. Pero a muchos nos cuesta cortar la cantidad justa de papel para cubrir incluso esta forma tan sencilla.
A veces nos sobra mucho papel, que terminamos doblando de forma desordenada en los extremos, o nos quedamos cortos y necesitamos improvisar un trozo adicional para cubrirlo por completo.
Sin embargo, existe una fórmula ingeniosa desarrollada por Sara Santos, matemática del King’s College de Londres, que puede ayudar no solo a reducir el desperdicio de papel, sino también a que los patrones coincidan en las uniones.
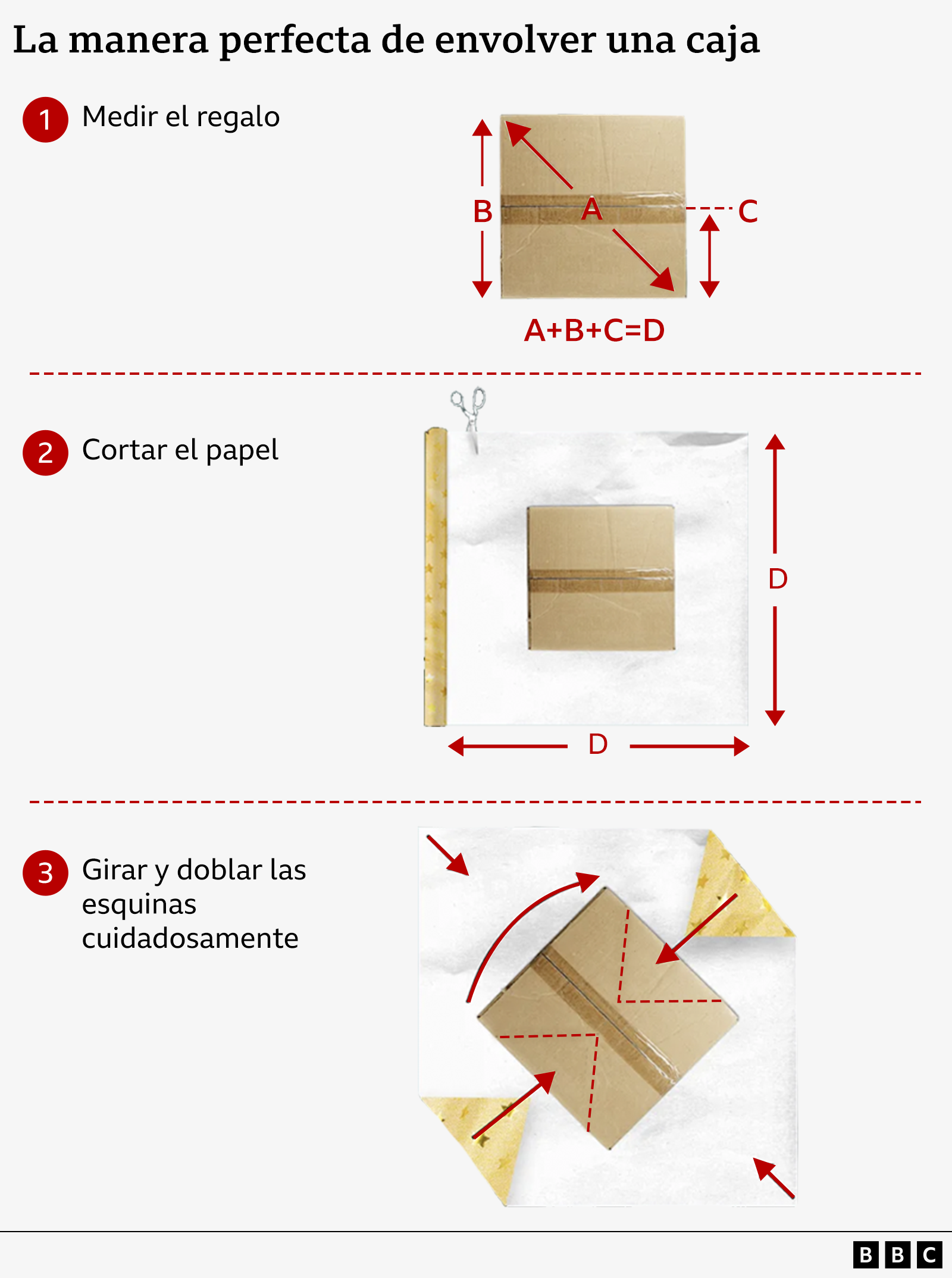
Primero, hay que medir la altura de la caja y multiplicarla por 1,5. Luego, se mide la diagonal del lado más grande de la caja, de esquina a esquina, y se suman ambas medidas. Esto proporciona las dimensiones del cuadrado de papel de regalo que se debe cortar.
Por ejemplo, si se va a envolver un cubo que mide 4,5 centímetros en diagonal y 3 cm de alto, hay que cortar un cuadrado de papel de 9 cm x 9 cm. Pero aquí viene el truco…
Cuando se coloca el regalo sobre el papel, hay que girarlo para que quede en diagonal en el centro. Luego, se dobla con cuidado las cuatro esquinas del papel hacia el centro, metiendo las solapas de cada esquina de la caja debajo de las más grandes al doblarlas.
Es importante asegurar el papel con solo tres trozos pequeños de cinta adhesiva y, si se usa papel a rayas, incluso es posible que el estampado coincida en las uniones.
Este método a veces también se puede usar para paralelepípedos.
“Sin embargo, si el papel es cuadrado, no siempre es cierto que el envoltorio diagonal sea mejor”, afirma Holly Krieger, profesora de matemáticas de la Universidad de Cambridge.
Explica, por ejemplo, que si una caja mide 2 x 4 x 8 cm, con el método diagonal se necesita un cuadrado de papel de 14 x 14 cm, pero es posible envolver el mismo regalo de forma más convencional con un cuadrado de papel de 12 cm.
El truco de la posición diagonal es más útil si se dispone de un trozo de papel cuadrado que no alcanza a cubrir un cubo de la forma tradicional.
Al colocarlo en diagonal, puede que sí se logre cubrir el regalo. De manera similar, los rectángulos de papel que no cubren completamente regalos con forma de paralelepípedo, como una caja de zapatos, se pueden adaptar si se coloca la caja en diagonal.
Solución práctica
Este método a veces también funciona para prismas triangulares.
Se mide la altura del triángulo en el extremo del empaque del prisma, se duplica y se suma la longitud total de la caja para obtener la medida perfecta de papel necesaria para cubrir sus extremos triangulares con tres capas de papel y lograr un acabado impecable.
Para envolver un tubo de caramelos u otro regalo cilíndrico con el mínimo desperdicio de papel, hay que medir el diámetro del extremo circular y multiplicarlo por por Pi (3,14…) para calcular la cantidad de papel necesaria para envolver el regalo.
Luego, se mide la longitud del tubo y suma el diámetro de un círculo para calcular la longitud mínima de papel necesaria.
De esta manera, el papel se unirá exactamente en el centro de cada extremo circular del regalo, requiriendo solo un pequeño trozo de cinta adhesiva para asegurarlo.
Sin embargo, es mejor dejar un poco de papel extra para asegurarse de que la forma quede completamente cubierta y evitar arruinar la sorpresa.

Volviendo al tema…
Si el regalo es una pelota, ¡mala suerte! Las esferas son, sin duda, la forma más difícil de envolver.
Es imposible cubrir una pelota de manera uniforme con un trozo de papel, no solo porque las propiedades del papel impiden que se doble infinitamente, sino también por el teorema de la bola peluda, explica Sophie Maclean, divulgadora de matemáticas y estudiante de doctorado en el King’s College de Londres.
Este teorema explica que es imposible peinar el pelo de una bola o esfera de forma que quede liso sin crear al menos un remolino o mechón rebelde.
“Si piensas en envolver una pelota con papel de regalo, no podrás conseguir que quede completamente lisa”, dice Maclean. “En algún punto habrá un bulto o un hueco”.
“Personalmente, me gusta ser creativa al envolver regalos, y en este caso lo aprovecharía. Ata un lazo alrededor o retuerce el papel para que parezca un caramelo o un regalo con forma de dulce”.
Si se busca la máxima eficiencia al envolver un balón de fútbol con papel, se puede probar usar un trozo de papel de aluminio con forma triangular.
Un equipo internacional de científicos estudió cómo se envuelven de forma eficiente los bombones Mozartkugel —esferas de mazapán recubiertas de praliné y bañadas en chocolate negro— con un pequeño trozo de papel de aluminio.
Observaron que minimizar el perímetro de la forma reduce el desperdicio, lo que hace que un cuadrado sea más eficiente que un rectángulo de la misma área.

Crear formas de pétalos es otra manera de cubrir una esfera de manera eficiente, aunque se necesitaría una cantidad infinita de pétalos para hacerlo con total precisión.
Sin embargo, los investigadores descubrieron que un envoltorio con forma de triángulo equilátero es aún más eficiente. “El ahorro del 0,1% del área podría resultar significativo para los millones de bombones Mozartkugel que se consumen cada año”.
Añadieron que puede haber una posible reducción del 20% en el material necesario para cubrir una forma esférica.
Probablemente todos hemos tenido dificultades para envolver regalos duros e irregulares, como una taza, que es un cilindro abierto con un asa que sobresale.
“No existe una fórmula matemática sólida que describa todas las formas posibles. Esta es una de esas situaciones en las que la experimentación es casi más útil que intentar describirlo rigurosamente de forma matemática”, dice Krieger.
Una solución podría ser combinar un regalo de forma difícil con otro para crear una figura más regular y fácil de envolver.

Máxima eficiencia sin escatimar recursos
Envolver dos regalos de tamaño similar juntos es más eficiente que envolverlos por separado, ya que requiere menos papel. Pero envolver dos regalos de formas o tamaños muy diferentes suele requerir más papel, según Krieger.
Se necesita paciencia y mucha prueba y error al agrupar formas. Incluso los matemáticos tienen dificultades.
Algunos “problemas de empaquetamiento”, como encontrar la forma más eficiente de empaquetar cuadrados idénticos dentro de un cuadrado o rectángulo más grande, se conocen como problemas “NP-difíciles”, lo que significa que son extremadamente difíciles o incluso prácticamente imposibles de resolver, aún con las computadoras más potentes.
Es un área de investigación sorprendentemente activa entre los académicos.

Ordenar esferas para que ocupen el menor espacio posible es una tarea endiabladamente difícil, así que no es de extrañar que nos cueste envolver una bolsa de pelotas de golf de forma eficiente.
Afortunadamente, los matemáticos se están ocupando del asunto, buscando la mejor manera de hacerlo.
Sin embargo, para aquellos con mentes ordenadas, la mejor solución hasta la fecha parece requerir un método de empaquetado desestructurado y bastante aleatorio, junto con algunos cálculos asombrosos.
Practicar el método de Santos puede ahorrar papel y cinta adhesiva, además de impresionar a tus familiares y amigos, pero a veces incluso los matemáticos se ven tentados a tomar atajos cuando se enfrentan a envolver regalos particularmente complicados, como pelotas.
“Quizás simplemente compre una caja”, bromea Krieger.

Haz clic aquí para leer más historias de BBC News Mundo.
Suscríbete aquí a nuestro nuevo newsletter para recibir cada viernes una selección de nuestro mejor contenido de la semana.
También puedes seguirnos en YouTube, Instagram, TikTok, X, Facebook y en nuestro nuevo canal de WhatsApp, donde encontrarás noticias de última hora y nuestro mejor contenido.
Y recuerda que puedes recibir notificaciones en nuestra app. Descarga la última versión y actívalas.






